Excel 2010 Matrix Multiplication (MMULT)
Previously we have covered how to evaluate the inverse of matrix. Now we will be using Excel inherent MMULT function to find out multiplication of matrix directly, rather than going for manual formulation. It also deals with data values as array and takes array as argument(s).
Launch Excel 2010 spreadsheet on which you need to find out matrix multiplication. For instance we have included a spreadsheet containing fields; Matrix1, Matrix2 and Multiplication as shown in the screenshot below.
We will be finding out the multiplication of the matrices. We have three 2×2 and one 3×3 matrix. The formula would be absolutely same for each category. The old method of evaluating multiplication could be very lengthy especially when we have got to deal with 3×3 matrix. But we will be using MMULT function The basic syntax of this functions is;
=MMULT(array1,array2)
The first and second argument of the function is a simple array, as it takes array as argument, we will be putting location of the cell where array is residing. However, you can also put in values directly.
We will write this function as;
{=MMULT(A2:B3, E2:F3)}
As A2:B3 is the location of the cell where our first matrix is residing and E2:F3 is the location of second one. As we have been dealing with array here, so you need to press Ctrl+Shift+Enter to enclose the function in curly brackets, that indicates the usage of arrays.
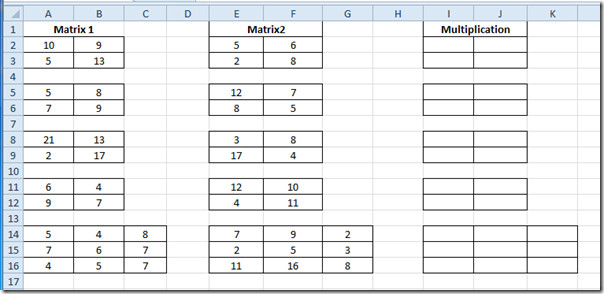
Now select the first matrix cells in Multiplication field and just enter the function as mentioned above. It will yield the multiplication result in 4 cells as we have been evaluating 2×2 matrix.
![mutiplication]](https://www.addictivetips.com/app/uploads/2010/04/mutiplication.jpg)
For finding out multiplication results in other matrices, select the evaluated matrix and just copy & paste into other 2×2 matrices. As shown below, that we have just copied the matrix into matrix beneath it.
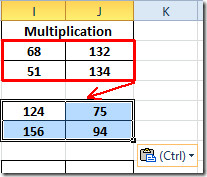
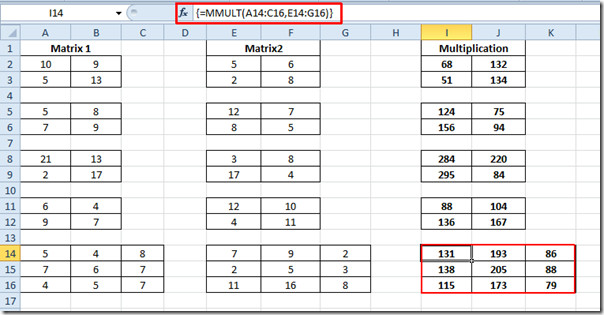
Now repeat the same procedure for all 2×2 matrices. For 3×3 matrix, Write down the function again, by providing each cell location in both matrices.
{=MMULT(A14:C16,E14:G16)}
You can also check out previously reviewed Matrix operation Function; Evaluating Matrix Determinant (MDETERM) and Finding out Inverse of Matrix.

muy bueno su tutorial muy didáctico