Office 2010: Fix Office Document Cache Error
Some people are getting the Document cache error while playing with their favorite office application. Those who upgraded from the Office Technical Preview to Office beta are facing this problem and the core reason behind this is that the office cache also needs to be upgraded. If you are for any reason getting this error, the quick steps listed below will instantly repair the problem.
First make sure that MSOSYNC.EXE process is not running, if so, kill it.
Now navigate to the HKEY_CURRENT_USER\Software\Microsoft\Office\14.0\Common\Internet and delete the FileStoreCriticalError key. If the key doesn’t exist then you can skip this step.
Make sure that the OfficeFileCache folder does not exist in the system. Please check the %userprofile% \AppData\Local\Microsoft\Office\14.0\ path and be sure to delete OfficeFileCache if it exists. %userprofile% is usually C:/Users/[UserName]/.
Once done, restart Office 2010 and the error should be gone. Enjoy!
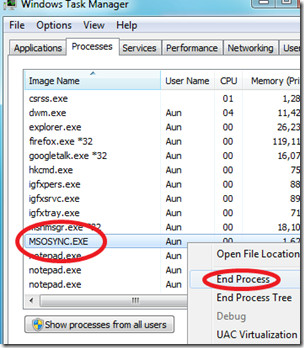
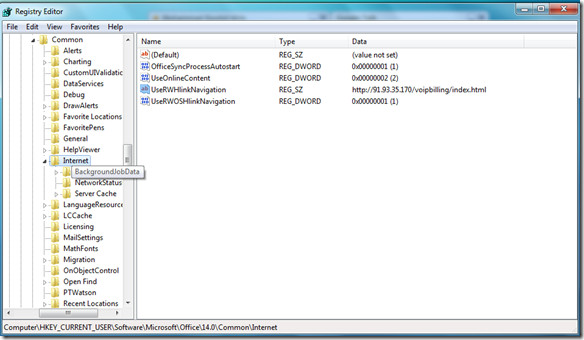

I had to boot to Safe Mode to be able to get rid of the cache – otherwise it kept telling me that the directory was in use by another program. Boot to safe mode (press F8 at boot, select “Safe Mode with Networking”, login with your normal user account and open a command prompt. Do this:
cd %userprofile%appdatalocalmicrosoftofficexx.0
The xx.0 will vary for your Office Version – 2013 is 15.0, 2010 is 14.0. Then do:
delnode OfficeFileCache
and make sure it is gone. If you can’t delete it, renaming it to “OfficeFileCache.BAD” like this:
REN OfficeFileCache OfficeFileCache.BAD
will probably do the trick – it doesn’t matter if it’s there, it’s just that Office has to not see it.
%userprofile% AppDataLocalMicrosoft
The path exists till here.. what after is different.. any tip?
I tried to delete the Office File Cache folder, but there were 2 files inside that would not be deleted or renamed or anything. Rebooted into safe mode and still could not do it.
So here’s my workaround that may work for some people. I did a system restore, just went back about 2 weeks (before the upload center stopped working), and when the machine rebooted, it was interesting that the upload center came up right away and said it needed to be repaired. This had NOT WORKED before, but I tried it one more time and this time it did the repair and then the error was gone and things were good again.
I wished I’d thought of doing this earlier – this was a 2-hour project trying these different things!
Thanks for the post. For office 2013 the reg key that needs to be removed is faultinformationstore
It worked, great! Thank you.
Thank YOU!!!!!!!!!!