Excel 2010: Password Protect Spreadsheet
The two mostly used protection levels in Excel are Worksheet Protection and Workbook Protection. Sometimes these two terms mean the same but actually differs from each other.
From Worksheet protection you can have a total control of spreadsheet or datasheet, by protecting each element your worksheet encompass. In this level of protection you can prevent users from modifying data, cells, formula, name ranges, etc.
By using Workbook protection level you can only lock-down the structure and worksheet window, which enables you to prevent spreadsheet from any structural change or from any change in size. In this post we will be covering some prominent ways of protecting spreadsheet.
There are several ways of protecting sheet, we will be putting light on each level of security which Excel 2010 provides. We have a datasheet which we want to protect from external use.
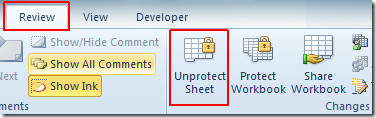
Now navigate to Review tab, under Changes group you will see Protect Sheet and Protect Workbook.
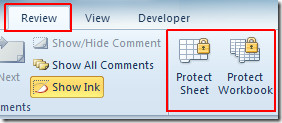
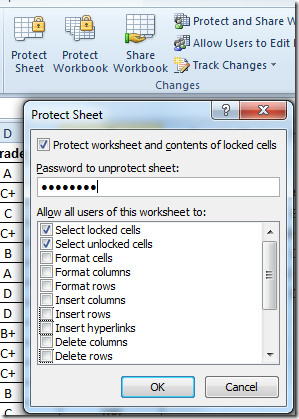
Click Protect Sheet, in the bottom pane of the dialog, enable those options against which you allow users to perform actions. Now enter a passphrase to protect worksheet and click OK.
When any user will try to hamper your spreadsheet, Excel preventive message will pop-up.

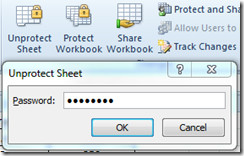
To make changes you need to first Unprotect the worksheet. For this navigate to Review and click Unprotect Sheet.
Upon click, it will ask you to enter the correct password.
Once done, the Unprotect Sheet button will change to Protect Sheet, informing you that now you can make changes in the spreadsheet.
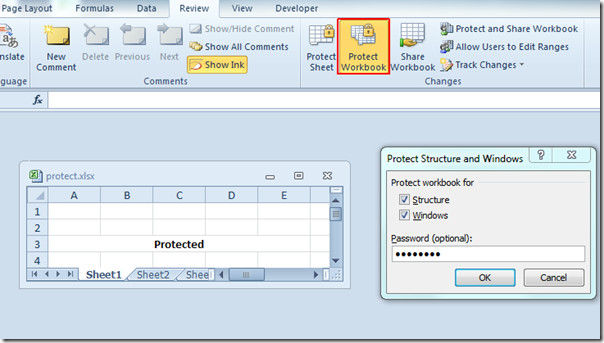
Now for protecting Excel worksheet window and it’s structure, navigate to Review tab and click Protect Workbook. We have to change the size of the spreadsheet window to give you an idea of this level of protection. Upon click, Protect Structure and Windows dialog will show-up, enable both options; Structure, and Windows. Enter a password to protect it and click OK.
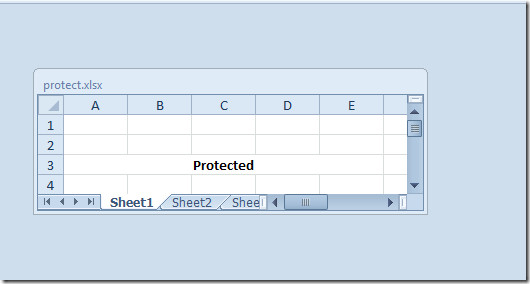
You will see that the structure and window size is locked-down, you can not change them unless you have sufficient rights. As you can see in the screenshot below that it cannot be moved, minimized, or maximized.
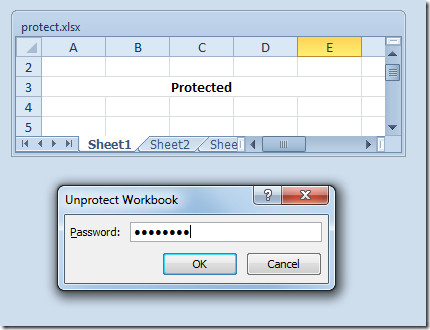
Clicking on Protect workbook again, you will be asked to provide a password to unprotect structure and window of Excel worksheet.
You can also check out previously reviewed guides on Insert Checkbox from control in Excel 2010 & Identifying Invalid Entries in Excel 2010.

(2007 Office user) – I had to (unshared the workbook), make a copy of the same workbook and ‘move to end’ of worksheets. I then was able to unprotect the worksheet(s) and unprotect the workbook using the password I originally created for the worksheet in question.
Hello everyone, I have a doubt… is there any option in excel in order to protect the workbook from editing, but at the same time the others should be able to add the data without being able to edit the data. Could you help me on this…
This is very helpful and simple to follow
Microsoft claim that excel spreadsheet are secure because their protection functions work with Excel.
Other .xlsx readers bypass their workbook protection as if they weren’t there.
But they still claim Excel is secure because they don’t make these other products.
I Spent a whole day trying to explain why my data was at risk, Is it a difficult concept?
Now I have to scrap weeks of work and scrap all MS products for ever!
Protection of sheets/book/VBA is really weak and is meant for joint work but not for data protection.
Real protection is Password to Open. Set this protection with a high-quality password and nobody will be able to get access to your data.
I mean Excel 2007 (xlsx files). Xls files (Excel 97-2003) can really be decrypted in a while (AccessBack/Decryptum).
We create fast GPU password recovery software and I’m sure in my words.
I am having issues getting a pasword protected workbook for excel 2013. In the past my spreadsheet was only viewable in “read only” if you didnt have a password. Excel would ask you the second you opened the spreadsheet. Does anyone know how to password protect a spreadsheet in excel 2013?
can excel auto prompt for a password on a single cell?
I protected excel sheet and forgot password……Any way to access?
Really nice article.. Thanks a lot for posting!
I am trying to make a workbook read only in a similar way that Office 2003 allowed it. I went to File > Info > Permissions > Mark as Final. This indeed makes the document read only, but it is very easy to click on “edit anyway” on the banner at the top of the document to modify it and save it again, overwriting the so-called previous final version.
With Office 2003, it was only possible to save a copy of an edited read only document. It seems to me that the option to mark as final is completely pointless in Office 2010.
I need to save an Excel document in a shared folder, but I want to prevent it being modified inadvertently by others who view it. However, as the owner of the document, I still want to modify it. This document contains pivot tables and charts that people will need to manipulate with the filters to display different types or results, so editing must be possible for them, just not saving their changes.
Is there a more efficient option than marking the document as final.
The quickest and most efficient way to do this is go to ‘File’ -> ‘Save As’ -> click on ‘Tools’ near the ‘Save’ button -> ‘General Options’ -> where you can create both ‘Password to open’ and ‘Password to modify’. Hope this is helpful. Good luck!
Correction, in Excel 2010 you don’t need to go to options, that takes you to another menu, the path is just File/Permissions/Encrypt
In Excel To prevent a file from opening without a password, you need Encrypt, not Protect (protect only prevents changes to a worksheet). They moved some of the menus around in the new version. go to File/Options/Permissions/Encrypt to password protect an Excel file
Above display is only to protect from editing the contents of your worksheet.Kindly follow Mr.Hugh’s instructions.It worked for me,only on giving the password you will be able to see the contents of the worksheet.
It still allows my spreadsheet to pop up, just makes me insert a password to change, that defeats the purpose of having it protected. I don’t want anyone to see this spreadsheet wo a password. What happened to the control from the previous version? This sucks.
I dont know if you got your reply yet but thanks to your comment, I got my answer. Using 2010 office pro plus; click file / info / Protect Workbook. Now no one can access this file without password.
It still allows my spreadsheet to pop up, just makes me insert a password to change, that defeats the purpose of having it protected. I don’t want anyone to see this spreadsheet wo a password. What happened to the control from the previous version? This sucks.
in office 2007 does not work protest on work book
plzzzz help me
my spreadsheet was set up as protected and used to ask for the passworkd but is not asking for the password now and it won’t allow me to unprotect.
The protect sheet and protect workbook tabs are greyed out.
How can I reset this so it is password protected again?
If I protect my excel spreadsheet with a password when i email the document to others as an attatchment can they open/print the document?
I just tried to send the same file as “Password Encrypted” and unprotected by password. The password protected/encrypted spreadsheet could not be opened by my Mac; the file without the password could be opened on my Mac. So if you find that the person receiving the file cannot open it, then you could remove the password and try sending it, although you might risk some loss of security by doing that.
its helpful.but i think, your english grammar is wrong.
Does not work for starter 2010.. no such button
I also have the same issue..did you find a solution?
How do you change the password?
I am working from Excel 2010, and am assuming that everything I see matches what you see:
Go to the “File” tab.Go to “Info” on the left-hand menu
Notice four buttons: Convert, Protect Workbook, Check for Issues, Manage Versions
Click on “Protect Workbook”
Click on “Encrypt with Password”
Then just type in the new password as if you were creating a password for the first time. You will then be prompted to enter the new password again.
Apparently, this also works for disabling the password: instead of typing in a new password, simply delete the password. This seems to take off the password protection.