Get Rid Of ‘ADB Shell’ Command With Enhanced Putty [Android Guide]
For Android users, ADB (or Android Debug Bridge) is the wonder toy. Most of the modifications, hacks and changes to the Android operating environment rely on the use of this debug bridge. Although now many tools have matured enough to skip the command line interface in favor of a GUI, nothing still beats the power of a manual command input, and the manipulation that it brings. Hence the ADB still remains developers’ favorite.
If you’re working with Linux, that’s one thing, but since most people use Windows, running the ‘adb shell’ command from standard Windows command line interface results in frustration and a blatant interface. Normally, a workaround is established in the form of running a telnet server on the Android device and using Putty in Windows to connect to that telnet server. This again, is not a very easy solution.
Thanks for senior XDA member sztupy, there is an easier way. The ADB itself sports a kind of terminal connection feature, which Putty can connect to directly. To get this working, you need to do quite a handful of manual adjustments. sztupy has compiled a Putty binary with most of the settings pre-set. Hence this Putty binary will give you a new connection type, ‘adb’, as shown in the screenshot below.
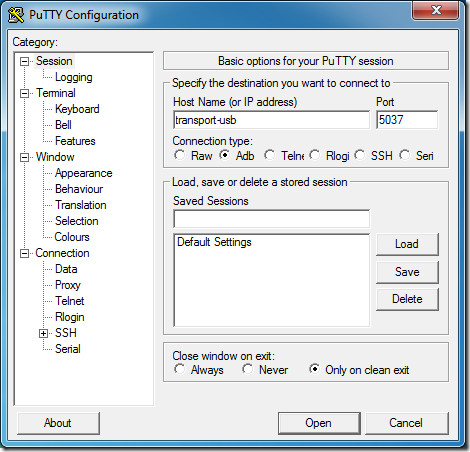
Here’s how you can connect your Android device for adb shelll command with sztupy’s modified Putty. Please note that you still need to have ADB installed on your machine – this is not a replacement tool for that.
- Put your Android device in USB Debugging mode and connect it to PC via USB cable
- Download the modified Putty binary here (https://www.addictivetips.com/app/uploads/software/adbputty.exe) mirror and run it
- Select ‘adb’ from connection type
- Enter ‘transport-usb’ (without quotes) in the ‘host’ field
- Enter 5037 as port (it should already be there, but enter manually if not)
That’s it. Hit the Open button to connect and enjoy adb shell command in a much better interface. You may want to save these connection settings in Putty for future connections.
For reference and more, check out the actual thread here on XDA forums.

Nice one! I feel much more comfortable using Putty then CMD.
Thank you, I was looking for tool where I can use CTRL+C in android shell. Modified putty works great! 🙂
Thank you, I was looking for tool where I can use CTRL+C in android shell. Modified putty works great! 🙂
This is great! I love it. Is there a way to connect to a specific device if there is more than one connected? Currently, it throws a “bad response” error if there are multiple devices connected. Thanks.
Add: The ADB server was not running.
I can’t get it to work. A window opens and, after a couple seconds, it closes.
so what about those of us who are forced to use wifi to use adb?
can this work??
Wifi people can use an app from the marketplace. I think it is called sshdroid.
I had a feeling that such a thing was possible! Thanks to the author of the modified Putty! And thank you for making us aware of it! Wonderful stuff!
That’s what i was looking for. Thanks!